Bất đẳng thức

Bất đẳng thức là một một mảng kiến thức khó và rộng trong chương trình toán THPT, vì vật hôm nay Toán Học xin chia sẻ đến bạn lý thuyết, phương pháp chứng minh các bất đẳng thức thường gặp và bài tập tự luyện kèm đáp án. Bài viết này sẽ bám sát kiến thức sách giáo khoa, đồng thời sẽ nêu những kiến thức cần ghi nhớ để giúp bạn đọc nhớ lâu, rèn luyện kĩ năng giải bài tập. Mời các bạn theo dõi

1. Lý thuyết bất đẳng thức

a) Bất đẳng thức là gì?

Cho a, b là hai số thực.

Các mệnh đề “a > b”, “a < b”, “a ≥ b”, “a ≤ b” được gọi là những bất đẳng thức.

b) Tính chất

c) Bất đẳng thức chứa dấu giá trị tuyệt đối

d) Bất đẳng thức Côsi

a) Đối với hai số không âm

Cho a ≥ 0, b ≥ 0, ta có $\frac{a+b}{2}\ge \sqrt{ab}$ . Dấu ‘=’ xảy ra khi và chỉ khi a = b

Hệ quả :

• Hai số dương có tổng không đổi thì tích lớn nhất khi hai số đó bằng nhau
• Hai số dương có tích không đổi thì tổng nhỏ nhất khi hai số đó bằng nhau

b) Đối với ba số không âm

Cho a ≥ 0, b ≥ 0, c ≥ 0, ta có $\frac{a+b+c}{3}\ge \sqrt[3]{abc}$. Dấu ‘=’ xảy ra khi và chỉ khi a = b = c

Lưu ý: Để hiểu sâu hơn về có thể xem lý thuyết và bài tập bất đẳng thức Cauchy ở phần trước

2. Các dạng bất đẳng thức

Dạng 1. Sử dụng định nghĩa và tích chất cơ bản

Để chứng minh bất đẳng thức(BĐT) A ≥ B ta có thể sử dụng các cách sau:

• Ta đi chứng minh A – B ≥ 0. Để chứng minh nó ta thường sử dụng các hằng đẳng thức để phân tích A – B thành tổng hoặc tích của những biểu thức không âm.
• Xuất phát từ BĐT đúng, biến đổi tương đương về BĐT cần chứng minh.

Ví dụ minh họa

Loại 1: Biến đổi tương đương về bất đẳng thức đúng

Ví dụ : Cho hai số thực a, b, c. Chứng minh rằng các BĐT sau

a) $ab\le \frac{{{a}^{2}}+{{b}^{2}}}{2}$

b) $3\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}} \right)\ge {{\left( a+b+c \right)}^{2}}$

c) ${{\left( a+b+c \right)}^{2}}\ge 3\left( ab+bc+ca \right)$

Lời giải

a) Ta có ${{a}^{2}}+{{b}^{2}}-2ab={{(a-b)}^{2}}\ge 0\Rightarrow {{a}^{2}}+{{b}^{2}}\ge 2ab$.

Đẳng thức$\Leftrightarrow a=b$.

b) BĐT tương đương $3\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}} \right)\ge {{a}^{2}}+{{b}^{2}}+{{c}^{2}}+2ab+2bc+2ca$

$\Leftrightarrow {{\left( a-b \right)}^{2}}+{{\left( b-c \right)}^{2}}+{{\left( c-a \right)}^{2}}\ge 0$ (đúng) ĐPCM.

Đẳng thức xảy ra <=> a = b = c

c) BĐT tương đương ${{a}^{2}}+{{b}^{2}}+{{c}^{2}}+2ab+2bc+2ca\ge 3\left( ab+bc+ca \right)$

$\Leftrightarrow 2\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}} \right)-2\left( ab+bc+ca \right)\ge 0$

$\Leftrightarrow {{\left( a-b \right)}^{2}}+{{\left( b-c \right)}^{2}}+{{\left( c-a \right)}^{2}}\ge 0$ (đúng) ĐPCM.

Đẳng thức xảy ra <=> a = b = c

Nhận xét: Các BĐT trên được vận dụng nhiều, và được xem như là “bổ đề” trong chứng minh các BĐT khác.

Loại 2: Xuất phát từ một BĐT đúng ta biến đổi đến BĐT cần chứng minh

Đối với loại này thường cho lời giải không được tự nhiên và ta thường sử dụng khi các biến có những ràng buộc đặc biệt

Ví dụ: Cho a,b,c là độ dài ba cạnh tam giác. Chứng minh rằng:${{a}^{2}}+{{b}^{2}}+{{c}^{2}}<2(ab+bc+ca)$.

Lời giải

Vì a,b,c là độ dài ba cạnh tam giác nên ta có $a+b>c\Rightarrow ac+bc>{{c}^{2}}$.

Tương $bc+ba>{{b}^{2}};\text{ }ca+cb>{{c}^{2}}$ cộng ba BĐT này lại với nhau ta có đpcm

Dạng 2: Tìm giá trị nhỏ nhất, lớn nhất và chứng minh bất đẳng thức bằng bất đẳng thức Cauchy 

Khi sử dụng bất đẳng thức Cauchy ( Cauchy ), bạn cần nhớ kĩ 4 lưu ý sau đây:

Ví dụ 1: Cho a, b là số dương thỏa mãn ${{a}^{2}}+{{b}^{2}}=2$. Chứng minh rằng $\left( \frac{a}{b}+\frac{b}{a} \right)\left( \frac{a}{{{b}^{2}}}+\frac{b}{{{a}^{2}}} \right)\ge 4$

Lời giải

Ví dụ 2: Tìm giá trị nhỏ nhất của các biểu thức sau$A=\frac{{{x}^{2}}-x+3}{\sqrt{1-{{x}^{3}}}}$ với $x<1$

Lời giải

Ví dụ 3: Cho a, b, c là các số thực dương. Tìm giá trị lớn nhất của $P=\frac{\sqrt{bc}}{a+2\sqrt{bc}}+\frac{\sqrt{ca}}{b+2\sqrt{ca}}+\frac{\sqrt{ab}}{c+2\sqrt{ab}}$

Lời giải

Dạng 3: Đặt ẩn phụ trong bất đẳng thức

Đặt ẩn phụ là một trong những kĩ thuật hay khi chứng minh bất đẳng thức, thể hiện được tính sáng tạo của người làm toán. Việc đặt ẩn phụ một cách khéo léo sẽ giúp ta đưa bất đẳng thức cần chứng minh trở thành những bất đẳng thức quen thuộc và dễ chứng minh hơn. Trong khuôn khổ nhất định của bài viết, chúng tôi xin đuợc trao đổi cùng các bạn về một số cách đặt ẩn phụ khi gặp một số bất đẳng thức đại số gồm 3 biến với giả thiết

Ví dụ 1: Cho các số dương a, b, c. Hãy chứng minh rằng $\frac{a+b}{a+b+c}+\frac{6b+8c}{2a+b}+\frac{3a+2b+c}{b+c}\ge 7$

Lời giải

Ví dụ 2: Cho x, y, z là số dương thỏa mãn x + y + z ≤ 1,5. Chứng minh rằng $x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\ge \frac{15}{2}$.

Lời giải

Dạng 5: Sử dụng bất đẳng thức phụ

Điều quan trọng dạng toán này là cần phát hiện ra được bất đẳng thức phụ. Bất đẳng thức phụ có thể là những BĐT cơ bản đã có hoặc là chúng ta từ đặc điểm của BĐT cần chứng minh chúng ta dự đoán và đưa ra BĐT phụ từ đó vận dụng vào bài toán.

Ví dụ 1: Cho a, b, c là số dương. Chứng minh rằng: $\frac{a}{{{b}^{3}}}+\frac{b}{{{c}^{3}}}+\frac{c}{{{a}^{3}}}\ge \frac{a+b+c}{abc}$

Lời giải

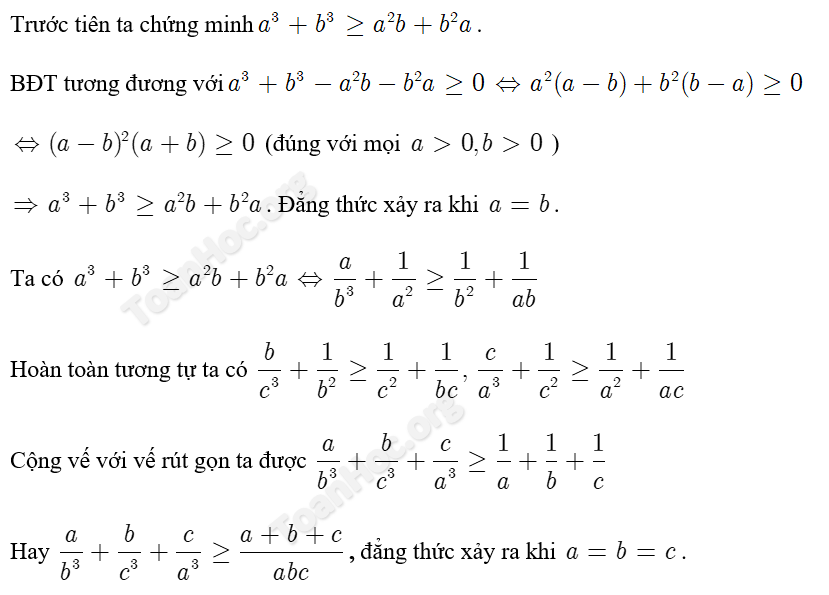
Ví dụ 2: Cho a, b, c dương thỏa mãn a + b + c = 1. Chứng minh rằng $\frac{a}{1+a}+\frac{b}{1+b}+\frac{c}{1+c}\le \frac{3}{4}$.

Lời giải

Để hiểu sâu hơn về bất đẳng thức bạn có thể tìm đọc bài bất đẳng thức côsi đã chia sẻ ở bài trước. Hy vọng bài viết này hữu ích với bạn đọc.