Trước đó bạn đã quen với tập hợp số thực, khi bước sang tập số phức sẽ khiến bạn gặp nhiều khó khăn. Không cần quá lo bởi bài viết này sẽ hệ thống đầy đủ lý thuyết số phức, các dạng bài tập số phức từ cơ bản tới nâng cao để bạn học – ôn tâp hiệu quả hơn.
1 Số phức là gì?
Số phức là số được có dạng biểu thức z = a + bi. Trong đó:
- a là phần thực z
- b là phần ảo z
- i là số ảo với i2 = – 1
- Tập hợp các số phức kí hiệu là C
Chú ý: Với z = a + bi
- b = 0 => z = a cũng là số phức => Mỗi số thức đều là 1 số phức
- a = 0 => z = bi được gọi là số thuần ảo hay còn gọi là ảo
- Số 0 vừa là số thực vừa là số ảo
- Số đối của z = a + bi là – z = – z – bi
Từ những chú ý trên ta thấy R ⊂ C
2 Những công thức số phức cơ bản
Cho hai số phức z = a + bi và z’ = a’ + b’i
2.1 Phép cộng và trừ
- Phép cộng z + z’ = (a + bi) + (a’ + b’i) = (a + a’) + (b + b’)i
- Phép trừ z – z’ = (a + bi) – (a’ + b’i) = (a – a’) + (b – b’)i
- Hai số phức bằng nhau khi: z = z’ <=>a + bi = a’ + b’i hay a = a’ và b = b’
2.2 Phép nhân, chia
- Phép nhân: z.z’ = (a + bi).(a’ + b’i) = (aa’ – bb’) + (ab’ + a’b)i
- Nếu k là 1 số thực thì: k.z = k(a + b.i) = ka + kb.i
- Phép chia: $\frac{z}{{z’}} = \frac{{a + bi}}{{a’ + b’i}}$$ = \frac{{\left( {a + bi} \right).\left( {a’ – b’i} \right)}}{{\left( {a’ + b’i} \right).\left( {a’ – b’i} \right)}}$$ = \frac{{aa’ + bb’}}{{{{\left( {a’} \right)}^2} + {{\left( {b’} \right)}^2}}} + \frac{{ba’ – ab’}}{{{{\left( {a’} \right)}^2} + {{\left( {b’} \right)}^2}}}.i$
2.3 Biểu diễn số phức
Trong hệ toạ độ Descartes, ta có thể biểu diễn số phức z = x + y.i như sau:
- Trục hoành biểu diễn phần thực
- Trục tung biểu diễn phần ảo
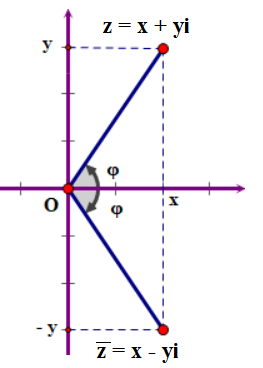
Mặt phẳng trên được gọi là mặt phẳng phức.
2.4 Số phức liên hợp
Số phức z = a + bi thì $\overline z $ = a – bi gọi là số phức liên hợp của z.
Tính chất:
- $z.\overline z = {a^2} + {b^2}$ là một số thực.
- $z + \overline z = 2a$ là một số thực
- $\overline {z + z’} = \overline z + \overline {z’} $
- $\overline {z.z’} = \overline z .\overline {z’} $
2.5 Module và Argument
Module: $\left| z \right| = \sqrt {z.\overline z } = \sqrt {{a^2} + {b^2}} $
- |z| ≥ 0, ∀z ∈ C
- Khi |z| = 0 => z = 0
- |z.z’| = |z|.|z’|
- $\left| {\frac{z}{{z’}}} \right| = \frac{{\left| z \right|}}{{\left| {z’} \right|}}$
- | |z| – |z’|| ≤ |z ± z’| ≤ |z| + |z’|
3. Dạng lượng giác của số phức
Từ số phức z = x + y.i ta có dạng lượng giác z = r(cosφ + isinφ), r > 0. Trong đó
- $r = \sqrt {{x^2} + {y^2}} $
- $\cos \varphi = \frac{x}{r}$
- $\sin \varphi = \frac{y}{r}$
- φ là 1 acgumen của z, φ = (Ox,OM)
|z| = 1 <=>cosφ + isinφ, với φ ∈ R
3.1 Những biến đổi lượng giác quan trọng
Giả sử có 2 số phức z = r(cosφ + isinφ) và z’ = r'(cosφ’ + isinφ’)
Phép nhân: z.z’ = r(cosφ + isinφ).r'(cosφ’ + isinφ’) = r.r’.[cos(φ + φ’) + i.sin(φ + φ’)]
Phép chia: $\frac{z}{{z’}} = \frac{{r\left( {\cos \varphi + i\sin \varphi } \right)}}{{r’\left( {\cos \varphi ‘ + i.\sin \varphi ‘} \right)}}$$ = \frac{r}{{r’}}\left[ {\cos \left( {\varphi – \varphi ‘} \right) + i\cos \left( {\varphi – \varphi ‘} \right)} \right]$
3.2 Công thức Moivre (Moa-vrơ)
- Lúy thừa zn = [r(cosφ + isinφ)]n = rn[cos(nφ) + isin(φ)], với n ∈ N*
- (cosφ + isinφ)n = cos(nφ) + isin(nφ)
3.3 Khai căn số phức dưới dạng lượng giác
Dạng tổng quát: $\sqrt[n]{z} = \sqrt[n]{r}\left[ {\cos \left( {\frac{{\varphi + k2\pi }}{m}} \right) + i.\sin \left( {\frac{{\varphi + k2\pi }}{m}} \right)} \right]$, với m = 0, 1, 2, 3, …, n – 1. (3.3.1)
Thường gặp dạng toán căn bậc 2 của số phức. Từ (3.3.1) ta thấy căn bậc 2 ứng với m = 2 – 1 = 1: $\sqrt z = \sqrt r \left[ {\cos \left( {\frac{{\varphi + k2\pi }}{1}} \right) + i.\sin \left( {\frac{{\varphi + k2\pi }}{1}} \right)} \right]$ $ = \sqrt z \left[ {\cos \left( {\frac{\varphi }{2}} \right) + i.\sin \left( {\frac{\varphi }{2}} \right)} \right]$