1. Hình thang là gì?
Một tứ giác lồi ABCD có hai cạnh đối song song với nhau (hình vẽ) thì tứ giác đó gọi là hình thang.
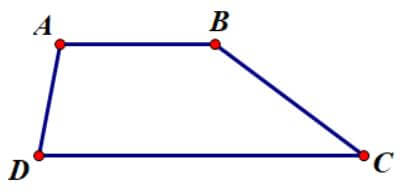
- Hai cạnh AB và DC song song với nhau gọi là hai cạnh đáy.
- Hai cạnh AD và BC là hai cạnh bên.
Bạn sẽ thường gặp 3 loại hình thang sau:
- Hình thang thường.
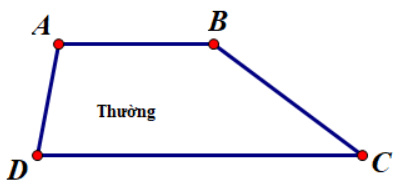
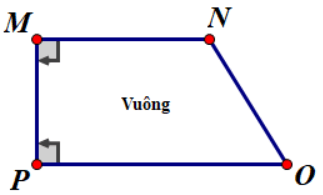
- Hình thang vuông là hình thang thường có 1 góc vuông
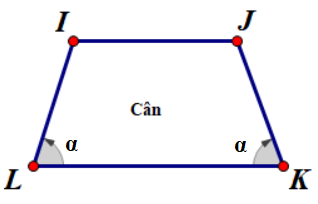
- Hình thang cân là hình thang thường có thêm hai góc kề một cạnh đáy bằng nhau và bằng α.
2. Công thức tính diện tích hình thang
Xét một hình thang bất kì biết hai cạnh đáy AB = a; DC = b và độ dài đường cao BQ = h

Muốn tính diện tích hình thang thì bạn sử dụng công thức: ${S_{ABCD}} = \frac{{a + b}}{2}.h$ (1)
3. Công thức tính diện tích hình thang vuông
Với hình thang vuông thì độ dài 1 cạnh bên chính là độ dài đường cao. Nghĩa là MN = a; OP = b và độ dài đường cao MP = h

Muốn tính diện tích hình thang vuông thì bạn sử dụng công thức:
${S_{MNOP}} = \frac{{a + b}}{2}.h = \frac{{MN + OP}}{2}.MP$ (2)
4. Công thức tính diện tích hình thang cân
Ta biết hình thang cân có 2 góc ở đáy bằng nhau và bằng α, ngoài ra độ dài hai cạnh bên cũng bằng nhau IL = JK.

Giống như tam giác thường, nếu biết độ dài đường cao h, hai cạnh đáy IJ = a; LK = b thì diện tích hình thang cân là
\[{S_{IJKL}} = \frac{{a + b}}{2}.h\]
Tuy nhiên ta có thể chia nhỏ hình thang cân như hình vẽ, sau đó cộng dồn các diện tích lại:
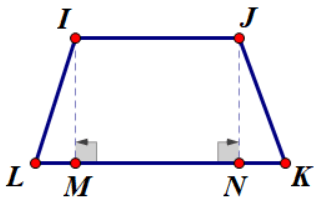
Công thức: SIJKL = SIML + SIJNM + SJKN = IJ.IM + IM.LM
5. Công thức tính chu vi hình thang
Giống như tứ giác lồi, chu vi hình thang bằng tổng độ dài bốn cạnh: CABCD = AB + BC + CD + DA
Trong đó:
- Độ dài hai cạnh đáy lần lượt là AB và CD
- Độ dài hai cạnh bên lần lượt là BC và DA
Chú ý: Giả sử gọi M là trung điểm của AB, N là trung điểm của CD thì đoạn thẳng MN gọi là đường trung bình của hình thang ABCD

6. Phân dạng bài tập
Dạng 1. Tìm diện tích khi biết đáy và đường cao

Dạng 2. Tìm tổng độ dài hai cạnh đáy khi biết diện tích S và chiều cao h

Dạng 3. Tìm chiều cao khi biết diện tích và độ dài hai cạnh đáy
